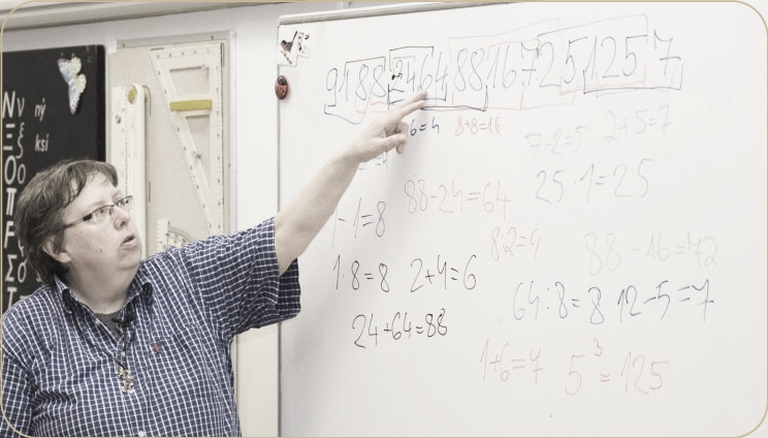
Abaku Start
Alena Vávrová
ZAČÍNÁME / Vytvoř číslo
Následné náměty jsou postaveny na principech metody Abaku a jsou určeny k postupnému rozvoji
početních dovednosti dětí. Nejsou časové náročné, a lze je tedy použít i na pouhou část hodiny.
Důkladná znalost principů abaku k tomu není nutnou podmínkou, je ovšem značnou výhodou, když je
vyučující zná.
Všechny aktivity jsou v souladu s Rámcovým vzdělávacím plánem a pomáhají naplňovat očekávané výstupy.
Konkrétně:
Pro 1. období: Čte, zapisuje a porovnává přirozená čísla, provádí zpaměti jednoduché početní
operace s přirozenými čísly.
Pro 2. období: Využívá při pamětném i písemném počítání komutativnost a asociativnost sčítání a násobení,
řeší a tvoří úlohy, ve kterých aplikuje osvojené početní operace v celém oboru přirozených čísel, řeší
jednoduché praktické slovní úlohy a problémy, jejichž řešení je do značné míry nezávislé na obvyklých
postupech a algoritmech školské matematiky.
Pro 3. období: Užívá ve výpočtech druhou mocninu a odmocninu, formuluje a řeší reálnou situaci pomocí
rovnic a jejich soustav, analyzuje a řeší jednoduché problémy, užívá logickou úvahu a kombinační úsudek
při řešení úloh a problémů, nalézá různá řešení předkládaných nebo zkoumaných situací.
Pokud s Abaku zkušenosti nemáte, začněte se cvičením Vytvoř číslo.
Nebojte se nabídnout aktivitu, která je primárně určena pro mladší děti, i dětem starším. Použijte
podle nich „jednoduchoučké“ příklady k oslabení averze k počítání, vytvořte si pohodlný nástup ke složitějším
aktivitám a pak i k samotné hře.
Základní cvičení „Vytvoř číslo“ obsahuje několik aktivit k seznámení s principem Abaku, všechny
jsou vhodné pro úplné začátky. Uvedený věk dětí je pouze orientační, vychází z toho, co by podle
RVP měly děti umět. V žádném případě nejde o horní hranici použitelnosti. V cvičení Trojice a
čtveřice můžete děti naučit vytvářet příklady bez znamének operací a rovnítek a přečíst příklad
„schovaný“ v troj- a čtyřciferném čísle. Tyto aktivity se vyplatí prolnout s náměty z městečka
Plusíkov.
Mezi dětmi napříč ročníky jsou velmi oblíbené řetězce a s nimi spojené vyhledávání příkladů v řadě
čísel. Zde máte k dispozici tři různé náročnosti řad, samozřejmě je přiloženo řešení. Poslední ze cvičení
zavádí zároveň s násobením a dělením také mocniny a odmocniny. Podívejte se, jak snadno třeťáci pracují
s druhou mocninou a odmocninou.
VYTVOŘ abakové číslo (pomůcka KARTY, MAGNETY, KAMENY)
Téma: Doplňování čísel tak, aby vznikl příklad aritmetické rovnosti (bez vyjádřených matematických
znamének).
Cíl (očekávaný výstup): Vytváření kombinací, hledání dalšího/dalších řešení.
Typická věková skupina: 6–7 let.
Návod k použití: Zadáme dětem dvě čísla (Abakarty). Způsob zadání je libovolný: napsat na tabuli nebo
ukázat na kartě, ale je vhodné, aby děti čísla viděly. Úkolem je doplnit třetí číslo tak, aby z čísel
bylo možno po doplnění znamének složit příklad.


Např. k zadaným číslům 2 a 5 lze doplnit 7 a získáme příklad 2 + 5 =7 (zapíšeme 257) nebo přidáme 3 a máme příklad 5 − 2 = 3 (zapíšeme 523).

U dětí se znalostí násobilky se už objeví i návrh na číslo 10, protože 2 · 5 = 10 (zapíšeme 2510).
Jestliže se objeví návrh na číslo 25, protože 5 na druhou = 25, využijte toho k zavedení pojmu
mocnin (viz aktivita Mocniny a odmocniny). Pokud už jste na toto téma řeč zavedli, zkuste je
dovést i ke kombinaci 25 (dvě na pátou), tedy k doplnění čísla 32.
Pozor: U čistě abakových kombinací se mocnina pomocí čísla dva nebo tři nepíše a vyšší mocniny se nepoužívají.
Nenechte se tím v tuto chvíli omezit a nechte děti dvojice čísel doplňovat libovolně. Je na vás, jaká
si stanovíte omezení. Podstatné je, aby děti dokázaly hledat a nacházet v libovolně zadané dvojici
čísel několik řešení.



Pro kontrolu: Doplním 3 (9 − 6 = 3) nebo 15 (9 + 6 = 15) nebo 54 (9 · 6 = 54)



Pro kontrolu: Doplním 4 (7 − 3 = 4) nebo 10 (7 + 3 = 10) nebo 21 (7 · 3 = 21).




Pro kontrolu: Doplním 4 (8 − 4 = 4) nebo 12 (8 + 4 = 12) nebo 32 (8 · 4 = 32) nebo 2 (8 : 4 = 2).
Vytvářejte si vlastní příklady i s vícecifernými čísly. Zapisujte vzniklé trojice (čtveřice…) jako
jedno číslo bez znamének operací a bez rovnítek.
TROJICE a čtveřice (pomůcka KAMENY, KARTY, KOSTKY)
Téma: Vytváření příkladů na sčítání a odčítání v rozsahu do deseti, vytváření příkladů s užitím
násobilky.
Cíl (očekávaný výstup): Naučit děti „vidět“ příklad v trojici (čtveřici) čísel bez zapsaných znamének,
procvičit počítání a vytváření příkladů, zlepšit jemnou motoriku manipulací s drobnými předměty.
Typická věková skupina: 6–7 let (1. třída), druhá část 9 let (konec 2., začátek 3. třídy).
Návod k použití: K aktivitě potřebujeme kameny s jednotlivými číslicemi (včetně nuly) tak, aby v kaž¬dé
sadě byla každá číslice alespoň 3krát. Číslíčka děti rozloží na lavici a vytvářejí z nich trojice tak,
aby z nich po doplnění znamének vznikl příklad. Podívejte se na obrázek. Vytvořenou trojici 718 čteme
„7 + 1 = 8“, trojici 936 čteme „9 − 3 = 6“.


Dodržujeme pořadí číslo – znaménko operace – číslo – rovnítko – číslo výsledku. Příklady čteme důsledně zleva doprava (popřípadě shora dolů). Ukažte na lavici na libovolnou trojici a nechte dítě příklad přečíst. Pozor na zpřeházená čísla, např. 374. Dítě v tom sice může vidět, že 3 = 7 − 4, ale trváme na výše uvedeném pořadí.
1. Zadejte první číslici. Další děti vyberou ze sáčku a vyrovnají do sloupce pod sebe a pak doplňují číslice do příkladu. Děti zcela přirozeně velice brzy překročí desítku. Nebraňte jim v tom, jen znova dohlížejte na správné uspořádání. Ukažte si, že když ve vytvořené trojici otočí pořadí kamenů, dostanou příklad s opačnou operací (např. 549/ 5 + 4 = 9 a 945/ 9 − 4 = 5).


2. Zadejte výsledek (v tomto uspořádání poslední číslo trojice) a děti vytvářejí příklady, které mají takový výsledek. Např. k číslu 8 doplňují 3 + 5, výsledný tvar je tedy 358.



3. Děti rozloží číslíčka na lavici a vytvářejí z nich čtveřice tak, aby z nich po doplnění znamének vznikl příklad. Podívejte se na obrázek. Vytvořenou čtveřici 5735 čteme 5 · 7 = 35.

4. Jako další varianty lze zadat první nebo druhou číslici či výsledek a doplňovat zbylé číslice. Můžeme trvat na tom, že skupiny kamenů musí být jenom čtyřciferné. Např. vyrovnejte na lavici do sloupečku deset dvojek a nechte děti doplnit příklady tak, aby byla dvojka na prvním místě. Všimněte si a výrazně oceňte toho, kdo kromě příkladů 2918 (2 · 9 = 18) nebo 2714 (2 · 7 = 14) vymyslí příklad 2874 (28 : 7 = 4).
5. Vezměte příklad – čtveřici kamenů (číslic) a sestavte z nich čtyři různé příklady, varianty
původního příkladu. Např.:
7321 (7 · 3 = 21)
3721 (3 · 7 = 21)
2137 (21 : 3 = 7)
2173 (21 : 7 = 3)




6. Naveďte děti k hledání takové čtveřice číslic, ze které jde poskládat více příkladů, např. čísla 2348 (základní příklad 3 · 8 = 24, druhý příklad 4 · 8 = 32). Oceňte s dětmi krásu matematiky

38 + 2 = 40 /3 · 8 = 24 / 8 : 2 = 4 / třetí odmocnina 8 = 2 / 2 na druhou = 4
7. Vyhlaste soutěž, kdo v časovém limitu sestaví nejvíce příkladů. Můžete požadovat příklady jen
na násobení nebo na dělení. Časový limit odhadněte podle rychlosti dětí. I když budou napoprvé
potřebovat ke složení deseti příkladů několik minut, velice rychle se zlepší. Je lepší dát
několikrát za sebou soutěž s kratším časem než jednu mnohaminutovou.
Máte okamžitý přehled, jak které dítě pracuje, protože skládané příklady a jejich množství vidíte přímo
na lavici.
VÝHONKY
Téma: Vytváření příkladů. (pomůcka Magnety / tabule - křída, křída, papír-tužka, kameny)
Cíl (očekávaný výstup): Kombinuje čísla k vytvoření abakového čísla.
Typická věková skupina: Bez omezení.
Návod k použití: Do sloupce pod sebe napíšeme jedno, a to samé abakové číslo a vytvoříme základní kmen.
Každý řádek můžeme rozvinou do delšího abakového čísla. Pro mladší děti volíme postupná růst rostlinky
s jednoduššími výpočty. Např.:
3263261
9003261226
326192
78326
32632626
29326
6523262
326193
15326127
… 326 : 326 =1
… 900 + 326 = 1226
… 32 . 6 = 192
… 78 : 3 = 26
… 32 – 6 = 26
… 29 – 3 = 26
… 652 : 326 = 2
… 32 + 61 = 93
… 153 – 26 = 27
Děti nejčastěji berou základní číslo jako celek a musíme je lehce navézt k tomu, aby se nebály rozdělit cifry původního čísla do jednotlivých členů příkladu nebo do výsledku. Společná práce u tabule je motivující a děti se předhánějí v složitějších příkladech.
ŘETĚZEC (pomůcka Magnety / tabule - křída, křída, papír-tužka, kameny)
Téma: Vytváření řetězců příkladů a obráceně hledání příkladů v řetězci čísel.
Cíl (očekávaný výstup): Naučit děti „vidět“ příklad ve skupině čísel bez zapsaných znamének.
Typická věková skupina: Všichni.
Návod k použití: Navážeme na aktivitu Trojice a čtveřice a Vytvoř abakové číslo. Hodinu je vhodné začít
použitím prvků z těchto aktivit, tj. skládat trojice, doplňovat číslo. Z trojic vytvořených na lavici
se s dětmi pokusíme vytvořit řetěz tak, aby se první a poslední číslo trojice překrývalo. Podívejte
se na obrázek:

Pokud spojovací čísla spojíme v jedno (dáme na sebe) vznikne řetězec 325496347183516. Zpětně
můžeme jít po řetězu a říkat příklady, ze kterých je řetězec spojen.
Zkuste rozdělit řetězec na jednotlivé příklady. Jsou dána čísla 4593617 a my v nich hledáme příklady
tak, že jednotlivé příklady musí být provázány v řetězci.
Podívejte se na obrázek:

Jedná se o příklad 4 + 5 = 9 ve zeleném oku, 9 − 3 = 6 v červeném a 6 + 1 = 7 v modrém řetězovém oku.
ABAKOVÉ ŘADY A: (pomůcka Magnety / tabule - křída, křída, papír-tužka, kameny)
Použijte pracovní list Řetěz A/ naleznete v metodice. Jsou to jednociferné příklady (tedy sčítání
a odčítání v oboru do deseti).
Napište (promítněte) dětem na tabuli jednu řadu a nechte je postupně zatrhávat (kroužkovat) a zapisovat
příklady. Naučte je používat pro přehlednost více barev. Nespokojujte se jenom se zatrháváním a příklady
vypisujte. Těm šikovnějším můžete dát rovnou celý pracovní list.
Všimněte si, že někdy jsou do dalšího příkladu použita dvě čísla a někdy jen jedno. Vytvořte vlastní
řadu. Vzhledem k tomu, že zatím zůstáváme u jednociferných čísel jak u zadání, tak u výsledku, je třeba
dát si pozor na některé kombinace. Jde hlavně o některá uspořádání s devítkou, např. 9817 (sice 9 −
8 = 1 a 8 − 1=7, ale také 9 + 8 = 17), 9716, 9615 atd., a ještě 1358 (13 − 5 = 8 a 3 + 5 = 8). Jsou
to pěkné kombinace a uplatníme je později.
Přehled nabídky pracovního listu Řetěz A:
1 + 2 = 3 / 3 + 5 = 8 / 8 − 6 = 2 / 4 + 5 = 9 / 9 − 6 = 3 / 3 + 4 = 7 / 7 − 2 = 5 / 2 + 3 = 5 / 6 − 2 = 4 / 6 − 3 = 3
2 5 7 1 6 3 9 1 8 3 5 1 4 2 2 7 9
2 + 5 = 7 / 7 − 1 = 6 / 6 + 3 = 9 / 9 − 1 = 8 / 8 − 3 = 5 / 5 − 1 = 4 / 4 − 2 = 2 / 2 + 7 = 9
3 5 8 1 7 1 6 1 5 3 2 1 8 9 3 6
3 + 5 = 8 / 8 − 1 = 7 / 7 − 1 = 6 / 6 − 1 = 5 / 5 − 3 = 2 / 1 + 8 = 9 / 9 − 3 = 6 / 3 − 2 = 1
4 3 7 2 5 1 4 5 9 2 7 6 1 5 3 8
4 + 3 = 7 / 7 − 2 = 5 / 5 − 1 = 4 / 4 + 5 = 9 / 9 − 2 = 7 / 7 − 6 = 1 / 5 + 3 = 8 / 1 + 4 = 5 / 6 − 1 = 5
5 2 3 3 6 9 5 4 2 2 6 8 4 4 3 1
5 − 2 = 3 / 3 + 3 = 6 / 9 − 5 = 4 / 4 − 2 = 2 / 2 + 6 = 8 / 8 − 4 = 4 / 4 − 3 = 1 / 3 + 6 = 9
6 3 9 2 7 4 3 1 4 5 9 8 1 6 7
6 + 3 = 9 / 9 − 2 = 7 / 7 − 4 = 3 / 3 + 1 = 4 / 4 + 5 = 9 / 9 − 8 = 1 / 1 + 6 = 7 / 4 − 3 = 1 / 1 + 4 = 5
7 1 8 4 4 3 7 2 9 3 6 1 5 1 4 3 7
7 + 1 = 8 / 8 − 4 = 4 / 4 + 3 = 7 / 7 + 2 = 9 / 9 − 3 = 6 / 6 − 1 = 5 / 5 − 1 = 4 / 4 + 3 = 7
8 1 9 6 3 3 2 5 7 6 1 1 2 6 8 5 3
8 + 1 = 9 / 9 − 6 = 3 / 3 + 2 = 5 / 7 − 6 = 1 / 1 + 1 = 2 / 2 + 6 = 8 / 8 − 5 = 3 / 6 − 3 = 3 / 2 + 5 = 7
9 5 4 3 1 1 2 4 6 2 8 1 9 7 2 2 4
9 − 5 = 4 / 4 − 3 = 1 / 1 + 1 = 2 / 2 + 4 = 6 / 6 + 2 = 8 / 8 + 1 = 9 / 9 − 7 = 2 / 2 + 2 = 4
Pozor: V 5. řadě je ještě příklad 6954 (6 · 9 = 54) a v 6. řadě 3927 (3 · 9 = 27) a 27431 (27 + 4 = 31). Pokud na to někdo z dětí přijde, chvalte, pokud ne, ani nedutejte. Při práci s dětmi zjišťujeme, že tam jsou další a další schované příklady. Platí předchozí věta.
ABAKOVÉ ŘADY B: (pomůcka Magnety / tabule - křída, křída, papír-tužka, kameny)
Použijte pracovní list Řetěz B/ naleznete v metodice. Každá řada obsahuje cca 10 příkladů hlavně
na sčítání a odčítání dvouciferných čísel, přičemž několik z nich je jednociferných (viz předchozí
řady). Tyto příklady děti najdou rychle, zvláště pokud už mají nějaké zkušenosti z předchozí
aktivity. Chvilku počkejte a dejte nejdříve příležitost slabším žákům.
Dejte jednu řadu za domácí úkol, až několik řad uděláte a děti budou vědět, co se po nich chce. Přidejte
řadu do písemné práce – uplatní se jako záchranný příklad. Každý v něm něco najde.
Příklady v řadě kroužkujte (zatrhávejte různými barvami), abyste viděli, že řetězec není přerušený.
Jednotlivé příklady zapisujte, budete mít lepší kontrolu, co už máte. Při vytváření vlastních řad dbejte
na provázanost. U řešení si všimněte, jak se jednotlivé příklady prolínají.
Přehled nabídky pracovního listu Řetěz B:
13 + 5 = 8 / 8 − 7 = 1 / 7 − 6 = 1 / 13 + 19 = 32 / 3 + 2 = 5 / 3 + 5 = 8 / 71 + 5 = 76 / 7 + 6 = 13 / 19 + 32 = 51
2 1 3 4 5 5 1 0 1 5 6 9 8 4 9 4 5
2 + 1 = 3 / 1 + 3 = 4 / 5 + 5 = 10 / 1 + 5 = 6 / 15 + 69 = 84 / 9 − 4 = 5 / 21 + 34 = 55 / 5 + 10 = 15 / 15 − 6 = 9 / 98 − 4 = 94
3 6 9 2 7 9 6 4 2 6 6 1 2 1 8 1 3
3 + 6 = 9 / 9 − 2 = 7 / 2 + 7 = 9 / 6 − 4 = 2 / 6 + 6 = 12 / 21 − 8 = 13 / 36 − 9 = 27 / 64 + 2 = 66 / 6 + 12 = 18 / 69 + 27 = 96
4 5 9 3 6 2 3 1 4 3 7 5 0 5 7 1 2
4 + 5 = 9 / 9 − 3 = 6 / 3 + 1 = 4 / 4 + 3 = 7 / 5 + 7 = 12 / 45 − 9 = 36 / 23 + 14 = 37 / 43 + 7 = 50 / 93 − 62 = 31 / 7 + 50 = 57
5 3 8 6 1 8 5 3 7 1 0 2 7 9 8 1
5 + 3 = 8 / 8 − 5 = 3 / 3 + 7 = 10 / 2 + 7 = 9 / 9 − 8 = 1 / 53 + 8 = 61 / 61 − 8 = 53 / 37 − 10 = 27 / 2 + 79 = 81 / 18 + 53 = 71
6 3 9 5 4 9 3 4 6 4 0 3 4 3 7 7 1 4
6 + 3 = 9 / 9 − 5 = 4 / 5 + 4 = 9 / 34 + 6 = 40 / 40 + 3 = 43 / 4 + 3 = 7 / 7 + 7 = 14 / 63 − 9 = 54 / 49 − 3 = 46 / 34 + 37 = 71 / 39 + 54 = 93
7 4 3 1 4 3 5 8 2 7 8 5 1 3 4 8
7 − 4 = 3 / 4 − 3 = 1 / 3 + 1 = 4 / 3 + 5 = 8 / 8 + 5 = 13 / 1 + 3 = 4 / 74 − 31 = 43 / 35 − 8 = 27 / 51 − 3 = 48 / 31 + 4 = 35 / 58 + 27 = 85
8 7 1 5 6 9 6 5 1 1 2 1 3 2 4 6
8 − 7 = 1 / 1 + 5 = 6 / 6 − 5 = 1 / 1 + 1 = 2 / 2 + 1 = 3 / 2 + 4 = 6 / 8 + 7 = 15 / 15 − 6 = 9 / 6 + 5 = 11 / 11 + 21 =32 / 56 + 9 = 65 / 11 + 2 = 13
9 2 7 4 3 1 2 3 5 4 9 4 5 9 9 1 8
9 − 2 = 7 / 7 − 4 = 3 / 3 − 1 = 2 / 2 + 3 = 5 / 4 + 5 = 9 / 9 − 1 = 8 / 4 − 3 = 1 / 1 + 2 = 3 / 5 + 4 = 9 / 27 + 4 = 31 / 31 + 23 = 54 / 54 − 9 = 54 / 94 + 5 = 99 / 9 + 9 = 18 / 9-1=8
Poznámka: V jednotlivých řadách se ještě přes veškerou snahu vyskytly i příklady na dělení, a to
ve 2. příkladu 551 (5 : 5 = 1), 4. příkladu 623 (6 : 2 = 3), 6. příkladu 771 (7 : 7 = 1) a 9.
příkladu 991 (9 : 9 = 1).
Ve všech řadách se vyskytují mocniny a odmocniny. Až se k nim dostanete (viz kapitola Mocniny), vraťte
se k řadám a zkuste je najít. Pokud v řadě děti (nebo vy) objeví další příklady, chvalte (jste chváleni).
ABAKOVÉ ŘADY C: (pomůcka Magnety / tabule - křída, křída, papír-tužka, kameny)
Použijte pracovní list Řetěz C/ naleznete v metodice.V něm už to nejsou jen jednociferné nebo dvojciferné příklady na sčítání a odčítání, ale využijeme všechny operace.
Přehled nabídky pracovního listu Řetěz C:
1 + 5 = 6 / 56 + 90 = 146 / 6 · 8 = 48 / 92 + 9 = 101 / 15 − 6 = 9 / 14 · 6 = 84 / 84 + 8 = 92 / 89 + 2 = 91 / 15 · 6 = 90
2 4 6 4 8 8 6 1 4 8 4 3 2 8 6 2
2 + 4 = 6 / 64 : 8 = 8 / 8 + 6 = 14 / 8 · 4 = 32 / 8 − 6 = 2 / 24 : 6 = 4 / 6 · 14 = 84 / 43 · 2 = 86 / 2 + 46 = 48 / 24 + 64 = 88
3 8 2 4 0 4 2 6 1 6 4 4 8 3 2 4
3 · 8 = 24 / 8 : 2 = 4 / 4 + 2 = 6 / 6 : 1 = 6 / 4 + 4 = 8 / 8 · 3 = 24 / 38 + 2 = 40 / 2 + 40 = 42 / 16 : 4 = 4 / 4 · 8 = 32 / 82 − 40 = 42
4 2 6 7 3 3 1 0 0 6 3 3 1 3 2 0
4 + 2 = 6 / 67 + 33 = 100 / 6 − 3 = 3 / 3 : 3 = 1 / 3 · 1 = 3 / 42 : 6 = 7 / 733 − 100 = 633 / 33 − 1 = 32 / 26 + 7 = 33 / 33 − 13 = 20
5 6 7 8 9 7 2 9 5 4 5 4 9 7 7 1
56 : 7 = 8 / 8 · 9 = 72 / 7 + 2 = 9 / 9 − 5 = 4 / 5 + 4 = 9 / 7 : 7 = 1 / 9 − 7 = 2 / 9 · 5 = 45 / 49 : 7 = 7 / 97 − 2 = 95 / 54 − 5 = 49
6 6 3 6 9 4 5 9 9 8 1 9 9 2 8
6 · 6 = 36 / 3 + 6 = 9 / 9 − 4 = 5 / 4 + 5 = 9 / 9 − 8 = 1 / 8 + 1 = 9 / 1 · 9 = 9 / 36 : 9 = 4 / 94 + 5 = 99 / 9 · 9 = 81 / 81 : 9 = 9 / 36 + 9 = 45 / 98 + 1 = 99 / 19 + 9 = 28
7 3 2 1 9 4 2 3 6 9 2 7 1 4 4 1
7 · 3 = 21 / 3 + 2 = 1 / 19 + 4 = 23 / 2 · 3 = 6 / 3 + 6 = 9 / 9 − 2 = 7 / 1 · 4 = 4 / 4 : 4 = 1 / 73 + 21 = 94 / 36 − 9 = 27 / 2 · 7 = 14 / 27 + 14 = 41
Všimněte si číslic 2 a 7 – jsou ve třech příkladech a pokaždé v jiné pozici: jednou je dvojka menšitel a sedmička výsledek, v dalším příkladu jsou obě čísla mezi sebou násobena a nakonec spolu tvoří jedno číslo. Zkuste s dětmi hledat další takové zajímavé skupinky.
8 6 4 8 1 3 4 4 7 3 7 2 1 4 5 8
8 · 6 = 48 / 1 + 3 = 4 / 73 − 72 = 1 / 1 + 4 = 5 / 86 + 48 = 134 / 44 − 7 = 37 / 3 · 7 = 21 / 72 −
14 = 58 / 81 − 34 = 47 / 7 · 2 = 14
9 8 1 7 2 9 4 6 2 4 4 9 6 1 5 5
9 − 8 = 1 / 7 + 2 = 9 / 6 − 2 = 4 / 1 · 5 = 5 / 9 + 8 = 17 / 17 + 29 = 46 / 4 · 6 = 24 / 24 · 4 = 96
/ 9 + 6 = 15 / 9 · 81 = 729 / 46 − 2 = 44
Dejte čísla blízko k sobě a stanou se magnetickou x magickou stavebnicí - podívejte se na řadu 4972981990:
7 + 2 = 9 / 9 – 7 = 2 / 98 + 1 = 99 / 1 · 9 = 9 / 72 : 9 = 8 / 81 : 9 = 9 / 72 + 9 = 81 / 81 + 9 = 90 / 729 : 81 = 9 / 8 + 1 = 9 / 497-298=199 / 9 na třetí = 729,...
Práce s řadami procvičuje všechny matematické operace, nedovolí dětem zůstávat jen v oblasti jedné operace, nutí je kombinovat číslice a vytvářet vhodná čísla. A i přes to všechno je to úžasně baví. Podívejte se na videa na našem webu. Konkrétně na první dva díly o abakových řadách. Zastavte video hned na začátku a prohlídněte si zadaný řetězec. Pokuste se v něm najít schované příklady a odhadněte, jak budou děti postupovat. A pak video pusťte dál.
Všímejte si rostoucí náročnosti zatrhávaných příkladů. Není to náhodné, i vaše děti při opakovaném
luštění k tomu dospějí. Na počátečních příkladech se uplatní i slabší žáci, zapojí se společně s
ostatními a zažijí si také svůj úspěch.
TIP redakce:) Abakuřada na rozcvičku. Jakmile učitel(ka) s dětmi vyřeší několik řad a děti rozumí principu
hledání příkladů, lze děti zapojit do tvoření řad. Žáci si sami vymyslí řady (každé na své úrovni)
a napíší je na papír spolu se svým jménem. Papírky odevzdají učitelce. Učitel(ka) na začátku každé
hodiny náhodně vybere jeden z papírků. Vybraný žák napíše svou řadu na tabuli a sám si se třídou moderuje
hledání příkladů. Učitel(ka) získá cca 2-4 minuty k zápisu do třídnice, kontrole docházky apod. Děti
se nastartují na počítání. Každý žák ví, že někdy na něj dojde řada, všichni žáci se na aktivitu těší
MÍČKY(pomůcka Pracovní listy Míčky 1 / Míčky 2)
Téma: Čtení trojciferných čísel, jejich porovnávání a třídění z různých hledisek, hledání
příkladů. Cíl (očekávaný výstup): Vytvořit u dětí hravý vztah k číslům, aby je při pohledu na ně
dokázaly nejen přečíst, ale i najít v nich schovaný příklad. Postupem času nebude ten příklad pro
děti schovaný, uvidí ho na první pohled.
Typická věková skupina: 6 let (sčítání a odčítání jednociferných čísel), 8 let (3. třída na trojciferná
čísla).
Návod k použití: Použijeme Míčky 1 nebo Míčky 2 a čísla / příklady (variace) dle svého vepíšeme - vvytiskneme - použijeme.
- Pokud pracujeme s prvňáky, hledáme míčky, která mají ve svém čísle schován příklad. Ten obsahuje
jednu matematickou operaci a rovnítko, vždy v tomto pořadí. Takové míčky (i čísla) nazveme abakové.
Například míček s číslem 347 je abakový, protože obsahuje příklad 3 + 4 = 7, míček s číslem 374 abakový
není, protože v něm příklad není v požadovaném pořadí.
- Tam, kde zavádíme trojciferná čísla a děti se je učí správně číst, začínáme tím, že děti čísla na
míčcích čtou, mohou je porovnávat a řadit podle velikosti. Pokud jste ještě nepoužili tento list k
hledání příkladů, využijte jej teď.
- Děti čtou čísla na míčcích a rovnou k nim říkají, jestli jsou abaková (z Plusíkova1), vybarvují abakové
míčky a barevně rozlišují míčky s příklady na sčítání a na odčítání.
- Připravte kombinace tří čísel tak, aby neobsahovaly žádný příklad - ale tak, aby změnou jednoho čísla
již příklad vytvořit šlo. Opravte jednu číslici, aby byl míček abakový. Porovnejte s dětmi, jak dalece
se v opravách shodly. Zdůrazněte a oceňte rozmanitost oprav.
Např. míček 141 není abakový a lze ho opravit na 541, 145, 111, 441 nebo 144. Svou roli samozřejmě
hrají i znalosti dětí (jestli už umí násobilku).
Na prázdné míčky zapíšeme abaková čísla, případně dokreslíme další míčky.
- Nadhoďte otázku, kolik je trojciferných abakových čísel. (Podrobněji je tento problém řešen v cvičení
Problémové úlohy / Registrační značky).
U mladších dětí klademe spíše otázky typu, která abaková čísla začínají jedničkou, dvojkou…, které
je nejmenší abakové číslo (112; pokud pracujeme s nulou, tak samozřejmě 101).
Necháme je uvažovat, jestli mohou být abaková čísla jednociferná nebo dvouciferná. Podle úrovně dětí
můžeme tuto otázku položit obráceně, tedy proč jednociferná nebo dvouciferná čísla nemohou být abaková.
Poznámky:
- Jestliže jste se už v nějaké aktivitě seznámili s městečkem Plusíkov, lze na označení míčků používat,
že jsou z Plusíkova.
- Metoda Abaku používá nulu pouze jako součást víceciferného čísla, nikdy ji nepoužívá samostatně.
U těchto míčků bych její běžné používání doporučila.
- Může se stát, že mezi dětmi se objeví znalost, že např. číslo 39 je abakové, protože 3 na druhou
je 9. Ano, v tom případě může být abakové i dvouciferné číslo – pochválíme.
MOCNINY A ODMOCNINY
Téma: Druhá mocnina a odmocnina.
Cíl (očekávaný výstup): Vytvoření představy o opakovaném násobení a jeho zápis jako mocniny, zavedení
odmocniny jako opačné operace k mocnině. Aplikace opakovaného násobení na výpočet mocniny. Typická
věková skupina: 10 let (3. třída) a starší.
Návod k použití: Mocniny a odmocniny se dostávají na řadu v učivu matematiky povětšinou v 8. třídě
základní školy. Vlastní pojem mocnin jsou však děti schopny zvládnout jako opakované násobení hned,
jak se seznámí s násobilkou. Příklady, kdy jsou oba činitelé shodné, je většinou zaujmou již na první
pohled. Řada z nich se krásně rýmuje, určitě znáte:
„3 · 3 je devět, kdo bručí, je medvěd“,
„5 · 5 je dvacet pět, obletíme celý svět“ nebo
„6 · 6 je třicet šest, rozjedem to o sto šest“.
V tuto chvíli se jedná jen o zavedení pojmu. Násobení dvou (tří) shodných činitelů nazveme druhá (třetí) mocnina. Využijte zájem dětí a zaveďte mocninu obecně jako opakované násobení.
1. Zaměřte se na mocninu dvou, protože násobení dvou není náročné a děti ho zvládnou, případně
mohou použít i sčítání dvou stejných čísel pod sebou.
Vyprávějte dětem indickou legendu o Sissovi ben Dahirovi, který prý vymyslel šachy. Ukázal svému králi,
že i malý pěšec (obyčejný lid) může rozhodnout o vítězství. Moudrý učenec Sissa ben Dahir si poté jako
odměnu za svou hru přál maličkost: aby mu král dal zrnka pšenice v takovém množství, že na první pole
šachovnice dá jedno zrnko, na druhé dvě, na třetí čtyři, na čtvrté osm a na všechna další vždy dvakrát
více zrníček než na předchozí pole. Zkuste s dětmi spočítat, kolik zrnek to obnášelo.
Pro kontrolu: Na šachovnici je 64 políček, počet zrnek je na každém dalším zdvojnásoben, což znamená
„krát dva“ – opakované násobení dvěma, na posledním políčku pak 263. „Na 63“ proto, že i když je políček
64, těch násobících kroků, přesunů na další políčko, je 63.
Tedy 263 = 92 233 72 036 854 775 808, všech zrníček posčítáno dohromady je18 446 744 093 709 551 615.
I když se nedopočítáte až ke konečnému výsledku, je pro děti překvapením, jak rychle počet zrnek roste,
a výsledné číslo je pro ně nepředstavitelné.
2. Odmocninu zavedeme jako opačnou operaci k mocnině. Stejně jako tvoří dvojici sčítání a
odčítání, násobení a dělení. „Odmocnina ze 49 je 7, protože 7 na druhou je 49.“
Děti se vší pravděpodobností vyrukují s odmocninou z čísel, která nejsou druhou mocninou přirozeného
čísla. Z malé násobilky vědí, že všechna čísla nelze dělit beze zbytku (nejsou tedy násobkem přirozeného
čísla).
Jsou tedy i čísla, která nemají celočíselnou odmocninu. K jich určení lze použít kalkulačku. Vyberte
s dětmi v rozsahu do 100 ta čísla, která lze odmocnit, tedy jsou druhou mocninou přirozeného čísla.
Mají děti zájem najít i jiná čísla? Podpořte je v tom.
3. Ukažte dětem, jak se správně zapisuje mocnina (horní index děti většinou znají z počítačových
textových editorů) a jak odmocnina. Určitě je zaujme, jak tento znak vznikl. (Původně se před
odmocňované číslo psalo slovo radix (kořen). Tedy asi takto: „radix(64) = 8“. Postupně se to
zkrátilo na samotné r, třeba „r(81) = 9“, a v podobě malého r už je vidět základ pro znak
odmocniny √.)
Spolu se znalostí násobilky umí děti druhou mocninu (a odmocninu) do deseti. Používáním v abakových
příkladech se naučí některé třetí mocniny a odmocniny, postupně přidají i druhé mocniny vyšších čísel.
Není nutné je to učit (drilovat).
4. Abakový zápis čísla předpokládá pouze druhou a třetí mocninu a odmocninu bez použití jakýchkoliv dalších symbolů, stejně jako u jiných příkladů. Konkrétně?
648 čteme jako „odmocnina z 64 je 8“.
6216 čteme jako „6 na třetí je 216“.
273 čteme jako „třetí odmocnina z 27 je 3“.

5. Ukážeme dětem, že řada příkladů s mocninami je v abakové podobě vyloženě pěkná a skrývá v sobě
další příklady:
7343 je 7 na třetí = 343 a 7 − 3 = 4.
2166 je třetí odmocnina z 216 = 6 a 1 · 6 = 6.
1255 je třetí odmocnina ze 125 = 5 a druhá odmocnina z 25 = 5.
Jeden z nejhezčích abakových příkladů: 97299 je 9na třetí = 729, 97 + 2 = 99, 9 + 7 = 2, třetí odmocnina
ze 729 = 9, 7 + 2 = 9.
Abakové číslo 2464 znáte už možná znáte z autíček v Plusíkově. Všimněte si, že v sobě skrývá další
dva příklady (pro kontrolu 2 na druhou = 4 a 4 na třetí = 64).
6. Další možná inspirace v metodice Plusíkov / Doprava a Ulice nebo v oddíle Kombo / Abakové a
logické řady.
Další návrhy na konkrétní nabídku další herní aktivity naleznete po rozkliknutí jednotlivých pomůcek,
které jsou s praxí metodou didakticky provázány.
Další návrhy na konkrétní nabídku další herní aktivity naleznete po rozkliknutí jednotlivých pomůcek, které jsou s praxí metodou didakticky provázány.
